
For example, "let P( x) be a polynomial" is a shorthand for "let P be a polynomial in the indeterminate x". Moreover, the functional notation is often useful for specifying, in a single phrase, a polynomial and its indeterminate. Formally, the name of the polynomial is P, not P( x), but the use of the functional notation P( x) dates from a time when the distinction between a polynomial and the associated function was unclear. Many authors use these two words interchangeably.Ī polynomial P in the indeterminate x is commonly denoted either as P or as P( x). However, when one considers the function defined by the polynomial, then x represents the argument of the function, and is therefore called a "variable". When the polynomial is considered as an expression, x is a fixed symbol which does not have any value (its value is "indeterminate"). The x occurring in a polynomial is commonly called a variable or an indeterminate. The graph of a polynomial function of degree 3

The word polynomial was first used in the 17th century. That is, it means a sum of many terms (many monomials).
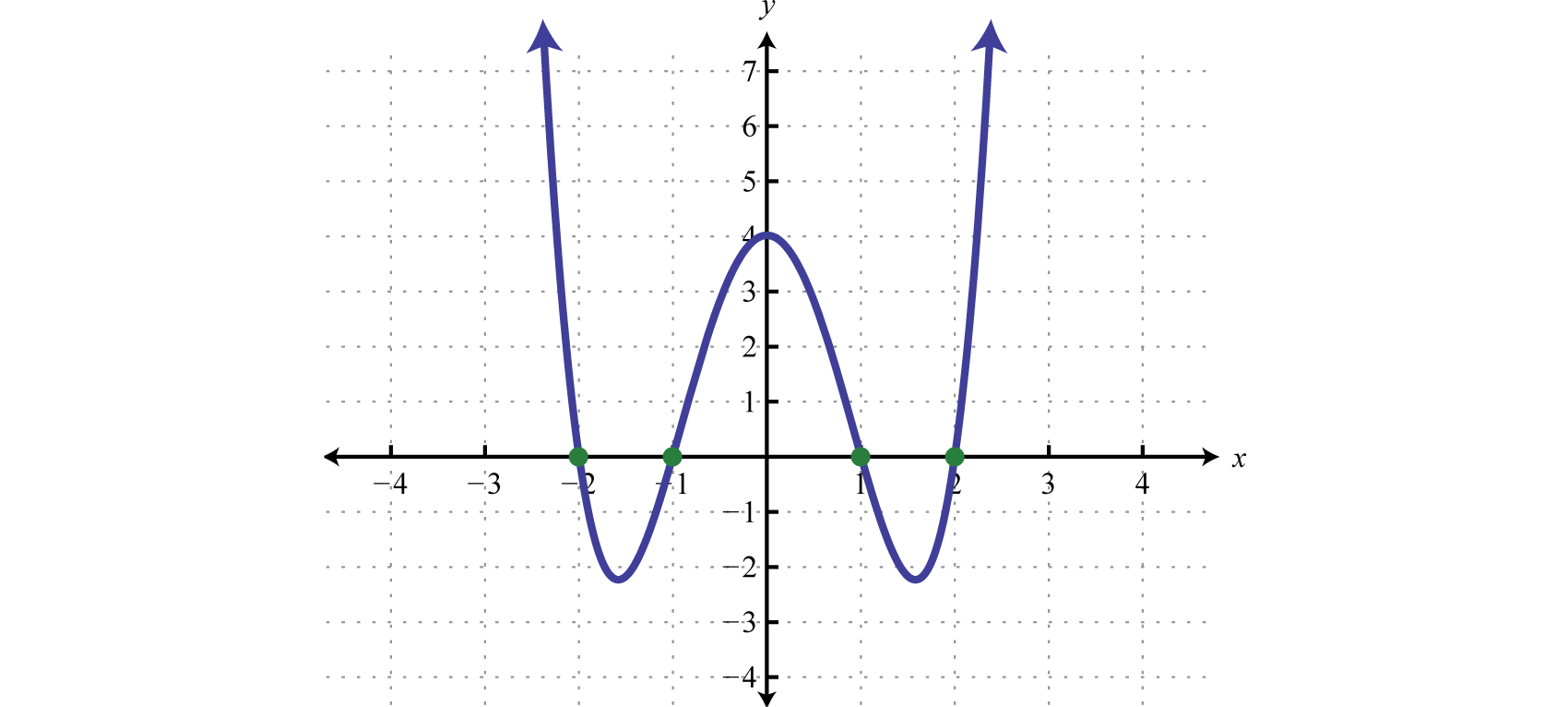
It was derived from the term binomial by replacing the Latin root bi- with the Greek poly. The word polynomial joins two diverse roots: the Greek poly, meaning "many", and the Latin nomen, or "name". In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science they are used in calculus and numerical analysis to approximate other functions. Polynomials appear in many areas of mathematics and science. An example in three variables is x 3 + 2 xyz 2 − yz + 1. An example of a polynomial of a single indeterminate x is x 2 − 4 x + 7. In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. The number of zeros of a polynomial is equal to a degree of a [polynomial.For less elementary aspects of the subject, see Polynomial ring.We can understand the shape of a polynomial on a graph using the degree of a polynomial.The concept of the degree of the polynomial can also be applied to the degree of equations.F9x)=0 is called the degree of the equation where f(x) is a polynomial.Read More : Important Notes on Polynomials Importance Of Degree Of Polynomials: To check whether the function is homogeneous or not.To find the number of maximum solutions, that function can have.To find the number of times, the function will cross the x-axis.Step-4: Check the largest power and that is the degree of variable x 9+x 2+x+x 0=9ĭegree is 8 Degrees Of Polynomial: Applications.


 0 kommentar(er)
0 kommentar(er)
